A Virtual Rubik's Cube
function M(x, ar =[]) {
return function go(func) {
if (func === dF3x) return x;
else if (func === dF3ar) return ar;
x = func(x);
ar.push(func.name);
return go;
};
} The default empty array "ar" was added to the basic m-M(x) closure to work with the function reverse() and the 24 name:inverse (key:value) pairs in ob.
function reverse () {
m(ob[m(dF3ar).pop()]); // Pops the key and runs m on value.
m(dF3ar).pop(); // Discard the function that m just pushed onto ar.
} The version of the m-M(x) closure used on this page encapsulates an array of six nine-member arrays of the strings "blue", "green", "red", "orange", "yellow", and "white." Users have at their disposal 12 basic functions (top row below) and their inverses (bottom row).
Pressing "U", "D", "R", "L", "F", or "B" keys, or clicking their corresponding buttons (above), rearranges some of the background colors of the 9 buttons that constitute each face of the virtual cube, simulating the result of turning the top, bottom, right, left, front, and back faces, respectively, of the virtual cube 90%. "M", "E", and "S" turn the middle sections 90 degrees. X", "Y", and "Z" turn the whole cube clockwise 90 degrees around the traditional x, y, and z axes. The single quote marks signify inverses, which can be run on the keyboard by simultaneously holding down the Shift key.
<button style="background-color: {m(dF3x)[3][3]}"
onclick={() => {m(Cyr)}} /> The elements of the array of six arrays held in the m-M(x) closure are embedded (by means of expressions "m(dF3ar)[j][k]") in the 27 buttons of the visible sides of the virtual Rubik's cube. If a user presses a key or clicks a button that calls m(func) -- thereby running x => func(x) in the m-M(x) closure -- each of the 27 copies of m in the method m (dF3ar) in the simulated Rubik's cube in the DOM immediately updates by returning the func(x). And if, for example, the string to which x[3][3] points in the closure changes from from 'green' to 'red', the value of m(dF3ar)[3][3] in the DOM will likewise change, and the color of the left square in the second row of the forward facing of the virtual Rubik's cube will be observed to change from red to green.
The nine strings of the array x[3] correspond exactly to the nine buttons constituting the front of virtual Rubik's cube. These are all orange on the starting and solved cube.
ddfunction reverse () {
m(ob[m(dF3ar).pop()]); // Pops the key and runs m on value.
m(dF3ar).pop(); // Discard the function that m just pushed onto ar.
} The object ob contains 24 key:value pairs of the names and inverses of the functions that exchange and rearrange the elements of the six nine-member arrays of strings that constitute x in the m-M() closure.
const ob = {'R': Rz, 'L': Lz, 'U': Uz, 'D': Dz, 'F': Fz, 'B': Bz, 'Cx': Cxr,
'Cy': Cyr, 'Cz': Czr, 'Xro': Xror, 'Yro': Yror, 'Zro': Zror, 'Rz': R,
'Lz': L, 'Uz': U, 'Dz': D, 'Fz': F, 'Bz': B, 'Cxr': Cx, 'Cyr': Cy, 'Czr': Cz,
'Xror': Xro, 'Yror': Yro, 'Zror': Zro}; Callbacks Rearrange x in the m-M(x) Closure
Clicking the "Start" button (or pressing "V") refreshes the m-M(x) closure by declaring "m = M(x)" where
x = [ ['blue','blue','blue','blue','blue','blue','blue','blue','blue'], // Right side ['green','green','green','green','green','green','green','green','green'], ['red','red','red','red','red','red','red','red','red'], ['orange','orange','orange','orange','orange','orange','orange','orange','orange'], // Front ['yellow','yellow','yellow','yellow','yellow','yellow','yellow','yellow','yellow'], // Top ['white','white','white','white','white','white','white','white', 'white'] ]
x[0], x[3], and x[4] correspond to the right side, front, and top faces of the cube, respectively. Pressing the "F" key calls m(F), causing the value of x (whatever it happens to be at the time) to update to F(x) in the m-M(x) closure. Corresponding to the rearrangement of x (see above), the front face of the cube will seem to have rotated clockwise 90 degrees. Here's the definition of "F."
The Browser Image
Here's the HTML code for the Rubik's cube image on the right:
<div class="face front">
<div class="grid">
<button style="background-color: {m(dF3x)[3][0]}" onclick={() => {m(Fz)}}/>
<button style="background-color: {m(dF3x)[3][1]}" onclick={() => {m(Cx)}}/>
<button style="background-color: {m(dF3x)[3][2]}" onclick={() => {m(F)}}/>
<button style="background-color: {m(dF3x)[3][3]}" onclick={() => {m(Cyr)}}/>
<button style="background-color: {m(dF3x)[3][4]}" onclick={() => {m(Zro)}}/>
<button style="background-color: {m(dF3x)[3][5]}" onclick={() => {m(Cy)}}/>
<button style="background-color: {m(dF3x)[3][6]}" onclick={() => {m(Fz)}}/>
<button style="background-color: {m(dF3x)[3][7]}" onclick={() => {m(Cxr)}}/>
<button style="background-color: {m(dF3x)[3][8]}" onclick={() => {m(F)}}/>
</div>
</div>
<div class="face right">
<div class="grid">
<button style="background-color: {m(dF3x)[0][0]}" onclick={() => {m(Rz)}}/>
<button style="background-color: {m(dF3x)[0][1]}" onclick={() => {m(Cz)}}/>
<button style="background-color: {m(dF3x)[0][2]}" onclick={() => {m(R)}}/>
<button style="background-color: {m(dF3x)[0][3]}" onclick={() => {m(Cyr)}}/>
<button style="background-color: {m(dF3x)[0][4]}" onclick={() => {m(Xro)}}/>
<button style="background-color: {m(dF3x)[0][5]}" onclick={() => {m(Cy)}}/>
<button style="background-color: {m(dF3x)[0][6]}" onclick={() => {m(Rz)}}/>
<button style="background-color: {m(dF3x)[0][7]}" onclick={() => {m(Czr)}}/>
<button style="background-color: {m(dF3x)[0][8]}" onclick={() => {m(R)}}/>
</div>
</div>
<div class="face top">
<div class="grid">
<button style="background-color: {m(dF3x)[4][0]}" onclick={() => {m(Uz)}}/>
<button style="background-color: {m(dF3x)[4][1]}" onclick={() => {m(Cx)}}/>
<button style="background-color: {m(dF3x)[4][2]}" onclick={() => {m(U)}}/>
<button style="background-color: {m(dF3x)[4][3]}" onclick={() => {m(Cz)}}/>
<button style="background-color: {m(dF3x)[4][4]}" onclick={() => {m(Yro)}}/>
<button style="background-color: {m(dF3x)[4][5]}" onclick={() => {m(Czr)}}/>
<button style="background-color: {m(dF3x)[4][6]}" onclick={() => {m(Uz)}}/>
<button style="background-color: {m(dF3x)[4][7]}" onclick={() => {m(Cxr)}}/>
<button style="background-color: {m(dF3x)[4][8]}" onclick={() => {m(U)}}/>
</div>
</div> Changing x in the m-M(x) JavaScript closure changes m(dF3x) embedded in the HTML code for the cube because they both point to the same place in memory. x === m(dF3x) returns "true." on in memory. Changing the value of x changes the value of m(dF3x) and vice versa.
The 27 buttons constituting the visible half of the simulated Rubik's cube never move. Pressing "Y" when the cube is in the starting configuration rearranges background colors to this configuration:

Press "Y" again and see this:

x[0] went from all blue (in the starting configuration), to all red (code is below) to all green (a little further down).
x = [ ['red','red','red','red','red','red','red','red','red'], // Right side
['orange','orange','orange','orange','orange','orange','orange','orange','orange'],
['green','green','green','green','green','green','green','green','green'],
['blue','blue','blue','blue','blue','blue','blue','blue','blue'], // Front
['yellow','yellow','yellow','yellow','yellow','yellow','yellow','yellow','yellow'], // Top
['white','white','white','white','white','white','white','white', 'white'] ]
And then ...
x = [ ['green','green','green','green','green','green','green','green','green'], // Right side
['blue','blue','blue','blue','blue','blue','blue','blue','blue'],
['orange','orange','orange','orange','orange','orange','orange','orange','orange'],
['red','red','red','red','red','red','red','red','red'], // Front
['yellow','yellow','yellow','yellow','yellow','yellow','yellow','yellow','yellow'], // Top
['white','white','white','white','white','white','white','white', 'white'] ]
x[3]'s background colors went from orange to blue to red. The cube seems to have rotated, but all of the divs and buttons remained stationary. Rearranging strings in the m-M(x) closure by pressing "Y", thereby rearranging the background colors of some of the simulated Rubik's cube buttons, created the illusion.
Move list length: ()=>v(b).lengthPressing the u, d, r, l, f, b, m, e, s, x, y, and z keys has the same effect as clicking the corresponding (capitalized) buttons. Holding down the "Shift" key (or activating "CapsLock") while pressing the keys causes the reverse effect. Pressing v, w, and q is equivalent to clicking Start, Scramble, and Reverse, respectively.
clicking either of two left corners of each face of the cube causes that face to seem to rotate counterclockwise 90 degrees. Clicking on either of two right corners of each face of the cube causes that face to rotate clockwise 90 degrees. clicking edges rotates center sections, rather than faces. clicking the centers of the right, top, and front rotates the entire cube clockwise on the X, Y and Z axes, respectively.
Of course, nothing actually rotates. Rearranging strings in the m-M(x) closure, thereby automatically rearranging the background colors of the buttons inside of the divs that constitute the virtual Rubik's cube, makes it seem that rotation occurred.
Some Algorithm Shortcuts
Press the "v" key or click Then click , , and buttons to see the main cube from various angles.
Continued from the previous page
Rotating the Left, Back, and Bottom Faces
METHOD ONE -- The fastest method:
The left, back, and bottom faces can be turned clockwise by pressing L, B, and D, respectively. Hold down the SHIFT key for counterclockwise rotation.
METHOD TWO -- clicking the cube
Click the top center 3 times to bring the green face forward.
Click the right top or bottom square.
Click the top center 3 more times, bringing
the red face forward.
Click
the right top or bottom square.
Click the top center two times to re-orient the cube.
Click the right center to bring up the
bottom face.
Click the right
top or bottom square.
Click the
right center 3 more times to re-orient the cube.
This is the expected result of pressing "LBD" or following the
instructions of Method 2 (above): 
The Amazing Reverse Function
Here's the function "reverse":
function reverse () {
m(ob[m(dF3ar).pop()]); // Pops the key and runs m on value.
m(dF3ar).pop(); // Discard the function that m just pushed onto ar.
} And this is the key-value lookup table:
const ob = {'R': Rz, 'L': Lz, 'U': Uz, 'D': Dz, 'F': Fz, 'B': Bz, 'Cx': Cxr,
'Cy': Cyr, 'Cz': Czr, 'Xro': Xror, 'Yro': Yror, 'Zro': Zror, 'Rz': R,
'Lz': L, 'Uz': U, 'Dz': D, 'Fz': F, 'Bz': B, 'Cxr': Cx, 'Cyr': Cy, 'Czr': Cz,
'Xror': Xro, 'Yror': Yro, 'Zror': Zro}; The array of six nine-member arrays of strings held in the m-M(x) closure is transformed whenever a user presses certain keys, or clicks the mouse over buttons or various parts of the displayed cube image. These actions call m(func) for functions "func" that rearrange strings in the m-M(x) closure, making it seem as though the virtual Rubik's cube, one of its six sides, or one of its three middle sections have rotated 90 degrees. This works because the strings in the m-M(x) closure are exposed in "background-color = m(dF3x)[j][k]" statements for 0 and positive integers j less than 6 and k less than nine, in the 27 buttons that constitute the visible faces of the virtual Rubik's cube seen in the browser.
Note: The attribute "key" added to the functions "func" discussed above are identical to the built-in string attributes "name." When trying to use "func.name," it was discovered that running "build" mutated names in the "ar" array in M, but an array of "func.name" emerged unchanged.
Some of the definitions of "func" in m(func) expressions (described above), can be found at Home. All of them are in the Github repository. Each time m(func) is called, func's key is appended to ar in M. Rapidly clicking "10,000 Scrambles" five times and waiting for it to finish indicates that 2,000,000 simulated 90 degree turns were performed and recorded in ar in around 3 seconds.
*********************************************************
I'll continue using SvelteKit, but I'm perturbed by having to add the attribute "key" to my functions when I would prefer to use the already-present attribute "name." Notice "func.name" in the definition of M at the top of this page. If "ar" in "M" contains "func.name" for each function that is called, SvelteKet renames many of them, causing the function "reverse" to fail.
Functions are objects in JavaScript. Here's a screenshot of simple function's internals taken in Firefox Developer Tools (accessed by pressing F12).
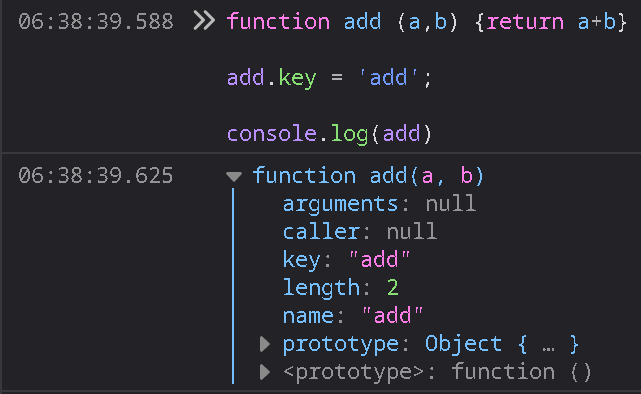
Why SvelteKit mangles arrays of func.name but not func.name escapes me. I'm glad that whoever "optimized" SvelteKit this way spared developer-added attributes.
*********************************************************
The efficiency of the "reverse" function can be observed by clicking "Scramble" or pressing the "W" key five times, and then holding down the "Q" key. You can watch the simulated cube perform 200 reverse moves in about five seconds.
function reverse () {
m(ob[m(dF3ar).pop()]); // Pops the key and runs m on value.
m(dF3ar).pop(); // Discard the function that m just pushed onto ar.
} The elapsed time is 0 milliseconds.
Move list length: ()=>v(b).length
function et2() {
var start = new Date();
let k;
for (k = 0; k < 10000; k++) {
shu();
}
elapsedTime = new Date() - start;
return elapsedTime;
}